Devoirs Hebdomadaire N°10
CDL...DH10
Compilation des Expressions Régulières (E.R.) en Automates finis (A.F.)
Expressions Régulières (E.R.)
Définition (inductive) : soit I un ensemble fini de symboles (un alphabet)
- a
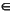 I alors
a est une E.R.
I alors
a est une E.R. - Si E1 et E2 sont des E.R. (E1 | E2) est une E.R. (union d'E.R.), E1E2 est une E.R. (concaténation d'E.R.) , E1* est une E.R. (ensemble des suites de longueur quelconque y compris 0 de E1 concaténées).
- il n'y en a pas d'autres
Remarques :
- une Expression régulière spécifie un ensemble dont les éléments sont des chaînes de symboles dont la construction respecte les règles (montrées dans l'ER).
- On note ^ l'E.R. vide ([] en Prolog).
Exemples d'ER :
I={a,b} E1= (a |
b)*abb E1 est
l'ensemble de toutes les suites de a et de b y compris de longueur 0
suivie de la chaîne abb.
I={a,b} E2=
101(01)* E2 est l'ensemble de toutes
les suites de 0 et de 1 alternés commençant par 1 et de longueur au
moins 3.
Analyse lexicale des E.R.
Remarque :
- les DCG travaillent sur des listes. Alors pour analyser une ER il faudra que cette ER soit sous forme de la liste de ses léxèmes (token).
- Pour simplifier les symboles de I seront des caractères.
- name(E , LL) transforme l'ER E (atome Prolog) dans la liste des codes ASCII de ses caractères.
On a écrit les prédicats ascii2carac/2 et lexER/2 pour réaliser l'analyse lexicale. lexER/2 retourne la liste des lexèmes de l'E.R. (caractères spéciaux et caractères de I):
ascii2carac([] , []) .
ascii2carac([ASCII|LASCII ], [C|LCARAC]) :- name(C , [ASCII]) , ascii2carac(LASCII, LCARAC) .
% cette analyse lexicale (un peu particulière) des ER est donc spécifiée par :
lexER(ER , LCARAC) :- name(ER , LASCII) , ascii2carac(LASCII, LCARAC).
Analyse syntaxique des E.R. :
Rappel : il faut d'abord analyser une ER pour vérifier qu'elle est correctement écrite (qu'elle est syntaxiquement correcte , qu'elle respecte la définition inductive).
gram1 : une DCG pour les ER :
er --> [X] , {member(X , I)}.
er --> ['('] , er , [')'] .
er --> er , ['|'] , er .
er --> er , er.
er --> er , ['*'].
Remarques :
- Cette grammaire est inutilisable avec les DCG de Prolog du fait de la récursivité gauche des productions 3 ,4 et 5.
- D'autre part on donne à '|' une précédence supérieure à la concaténation.
- D'où la grammaire gram1 revue et corrigée : gram2
er --> tr , ['|'] , er . % L'ER est un
Terme Régulier (tr) ou une ER
er --> tr. % L'ER est un Terme i.e. sans le symbole
'|' sauf entre '(' et ')'
tr --> fr , tr . % Le tr est un
Facteur Régulier (fr) concaténé à un tr
tr --> fr. % Le tr est un simple Facteur Régulier (fr)
fr --> [X] , { not member(X , ['(' , '[' ,
'|' , '*' , ']' , ')']) } , fer. % X n'est pas un symbole spécial
fr --> ['('] , er , [')'] , fer. % Le fr est une
er entre '(' et ')' suivie d'étoiles
fer --> ['*'] , fer. %des *, au moins une
fer --> []. % la chaine vide
QUESTION 1 : enregistrez gram2 dans un fichier Prolog avec les prédicats ascii2carac et lexER. et vérifiez que (a|b)*abb* est une ER bien écrite (syntaxiquement correcte).
remarque : poser la question ?- lexER('(a|b)*abb*' , LCARAC) , er(LCARAC , []).
On ajoute une règle dans la construction de E.R. : "sous E.R. optionnelle" :
Définition (inductive) devient : soit I un ensemble fini de symboles (un alphabet)
- a
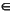 I alors
a est une ER
I alors
a est une ER - Si E1 et E2 sont des E.R. (E1 | E2) est une E.R. (union d'ER), E1E2 est une E.R. (concaténation d'ER) , E1* est une E.R. (ensemble des suites de longueur quelconque y compris 0 de E1 concaténées), [E1] est une E.R. (l'expression E1 est optionnelle (présente 0 ou une fois))
- il n'y en a pas d'autres
QUESTION 2 : modifiez gram2 pour obtenir gram3 en introduisant cette nouvelle règle dans l'analyse syntaxique et vérifiez que (a|b)*a[b]b est une ER bien écrite (syntaxiquement correcte).
Syntaxe Abstraite des ER :
on a choisi la syntaxe abstraite suivante : (rappel : l'E.R. vide est notée [] en Prolog)
Catégories syntaxiques :
e , e1 , ... pour les éléments de ER
a ,a1 , ... pour les éléments de I
Définitions :
e ::= a | conc(e1,e2) | ou(e1,e2) | star(e)
CONSTRUCTION de l'arbre de syntaxe Abstraite d'une ER :
Pendant l'analyse syntaxique on construit l'AST de l'ER analysée par : gram4 (gram3 augmentée de la construction de l'AST pendant l'analyse)
er(ou(TAST
, EAST)) --> tr(TAST) , ['|'] , er(EAST) .
er(AST) --> tr(AST).
tr(conc(FAST
, TAST)) --> fr(FAST) , tr(TAST) .
tr(AST) --> fr(AST).
fr(AST) --> [X] , { member(X , [a,b]) } ,
fer(ETOILE) , {zeroOUune(X , ETOILE , AST)}.
fr(AST) --> ['('] , er(AST1) , [')'] , fer(ETOILE) , {zeroOUune(AST1
, ETOILE , AST)}.
fer('*') --> ['*'] , fer(_). %une ou
plusieurs * est équivalent à une
fer([]) --> [].
zeroOUune(AST , * ,
star(AST)).
zeroOUune(AST , [] , AST).
QUESTION 3 : après avoir chargé gram4, quelle est la question pour obtenir l'AST de (a|b)*abb* ? Quel est cet AST ?
On ajoute la régle de l'E.R. optionnelle, d'où la définition supplémentaire dans la syntaxe abstraite :
e ::= a | conc(e1,e2) | ou(e1,e2) | star(e)| opt(e)
QUESTION 4 : modifiez gram4 96+gram5 introduisant la règle de l'E.R. optionnelle dans l'analyse syntaxique et la construction de l'AST et vérifiez que (a|b)*a[b]b est une ER bien écrite (syntaxiquement correcte) et donnez son AST.
Construction d'un Automates finis (A.F.) à partir d'une E.R.
Automate Fini :
Définition : un automate fini M est un quintuplet M = (S, I, d, s0, F)
S est un ensemble fini (d'états)
I est un ensemble (alphabet) fini (de symboles) d'entrée.
d : S x I ---> S est la relation de transition qui à un état et un symbole en entrée fait correspondre un état(s).
s0 un état particulier S (état de départ)
F sous ensemble non vide de S (ensemble des états finals).
exemple : M = ({s0,s1,s2,s3}, {a,b}, {d(s0,a)=s0 , d(s0,b)=s0 , d(s0,a)=s1, d(s1,b)=s2 , d(s2,b)=s3}, s0, {s3})
en Prolog on écrira :
depart(s0).
finals([s3]). % Attention les états finals forment un ensemble (représenté en prolog par une liste).
d(s0,a,s0 ).
d(s0,b,s0).
d(s0,a,s1).
d(s1,b,s2).
d(s2,b,s3).
Remarque : on peut représenter ces automates par un graphe, par exemple pour l'exemple précédent :
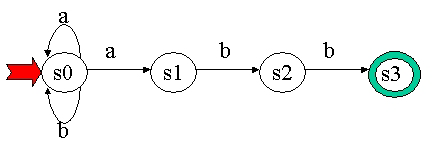
On généralise les transitions dans les Mouvements élémentaires d'un A.F. pour une chaîne de symboles : mve : SxI* ---> SxI* la relation qui fait passer l'AF de l'état s1 dans l'état s2 en "consommant" le premier symbole de la chaine en entrée par l'application d'une transition : mve(s1 , aC ) = (s2 , C) SSI d(s1 , a)=s2.
Soit mv la fermeture de mve : mv : SxI* ---> SxI* : mv(s1 , a1a0a1a2...aNC ) = (sN+1 , C) SSI il existe une suite (s0 , a0a2...aNC) , (s1 , a1...aNC) , ... , (sN , C) pour i=0, ... , N , mve(si , ai...aNC) = (si+1 , ai+1...aNC)
Définition : Reconnaissance d'une chaîne
un A.F. M reconnaît (accepte) une chaîne de symboles w=a1a0a1a2...aN de I* (ou élément de I*) SSI mv(s0, ai ) = (sf, ^) s0 l'état de départ , sf état final , ^ étant la chaîne vide.
Remarque :
- l'AF de l'exemple est NON-déterministe. En effet de s0 on peut atteindre s0 et s1 dans une transition par a.
- Prolog "et son backtrack" rend ces AF utilisables.
- Transition vide : on peut avoir mouvement élémentaire de l'AF sans consommation de symbole (mouvement spontané ?). On a alors une transition vide , notée d(S1 , ^ , S2), ^ étant la chaîne vide.
- Les transitions vide du type d(S , ^, S) ne servent à rien et seront supprimées.
Définition : Langage reconnu par un AF M=(S, I, d, s0, F)
c'est l'ensemble des chaîne reconnues par l'AF : L(AF)={w de I* | mv(s0 ,w)=(sF , ^) sF état final}
en Prolog :
mve((E1 , [X|LX]) , (E2,LX)) :- d(E1 , X , E2).
mve((E1 , LX) , (E2,LX)) :- d(E1 , [] , E2) , E1\=E2.
mv((E1 , LX1) , (E2 , LX2)) :- mve((E1 , LX1) , (E2 , LX2)).
mv((E1 , LX1) , (E2 , LX2)) :-
mve((E1 , LX1) , (E3 , LX3)) ,
mv((E3 , LX3) , (E2 , LX2)).
reconnaissance(CHAINE) :-
depart(S0),
mv((S0 , CHAINE) , (SF , [])),
finals(EF) , member(SF , EF).
|
QUESTION 5: chargezl'AF de l'exemple et les prédicats de reconnaissance sous Prolog et vérifiezque la chaîne ababababababababaabb est reconnue par l'AF.
ATTENTION : la chaîne ababababababababaabb doit être présentée sous forme d'une liste de symboles
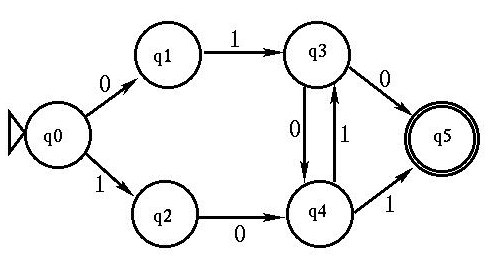
QUESTION 6: Donnez l'AF M01=(S , I , d , s0 , F) correspondant au graphe suivant i.e. précisez S , I , d , s0 et F : (l'état supportant une flèche est l'état de départ. Les états entourés d'un double cercle sont les états finals) et donnez deux exemples de chaînes acceptées par cet A.F. (chargez la version Prolog de l'A.F. et les prédicats de reconnaissance et montrez la reconnaissance de 2 chaînes en Prolog).
ER et AF :
Théorème : il existe une ER qui décrit le langage reconnu par un AF et inversement on sait construire un AF qui reconnait le langage décrit par une ER.
exemple : (a|b)*abb décrit le langage reconnu par

Construire un A.F. à partir d'une E.R. (compiler les ER en AF ) :
On va utiliser l'algorithme de Thompson qui à chaque sous arbre de l'AST d'une E.R. fait correspondre un schéma d'A.F. L'algorithme de Thompson de transformation d'une ER en AF produit des AF "fortement" NON déterministes (beaucoup de transitions vides) et qui ont la particularité d'avoir un seul état terminal dont ne sort aucune transition.
Rappel : A chaque définition de la syntaxe abstraite des ER correspond un schéma d'automate :
| E.R. | Graphe | A.F. correspondant |
| a | 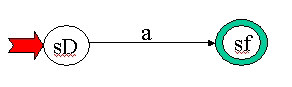 |
M = ({sD,sf}, {a}, {d(sD,a)=sf}, sD, {sf}) |
| conc(E1,E2) |
 |
M= (SE1 v SE2,
IE1 v IE2, dE1 v dE2
v {d(sf1,^)=sD2}, sD1, {sf2})
Attention les ensembles d'états SE1 et SE2 doivent être distincts |
| ou(E1,E2) |
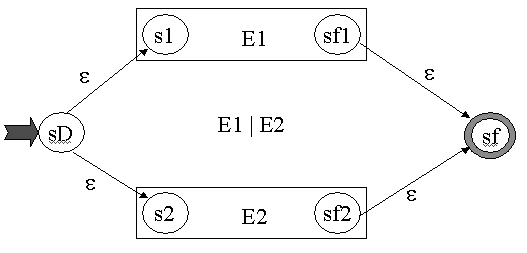 |
M= (SE1 v SE2
v {sD,sf}, IE1 v IE2,
dE1 v dE2 v sD, {sf}) Attention sD et sf sont de nouveaux états |
| star(E) |
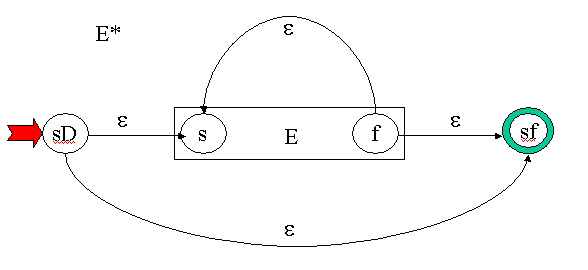 |
M= (SE v {sD,sf}, IE
,
dE v {d(sD,^)=sf , d(sD,^)=s , d(f,^,)=sf), d(f,^)=s}, sD, {sf}) Attention sD et sf sont deux nouveaux états |
Règles d'inférence Prolog de Construction d'un A.F. à partir d'une E.R. :
on définit -ER2AF-> : ER ---> AF qui à partir d'une E.R. construit un A.F.
en Prolog :- op(777 , xfx , '-ER2AF->').
Dans 3 règles sur 4 on crée de nouveaux états. Il faut donc en Prolog un générateur de symboles , un prédicat qui retourne un nouveau symbole à chaque appel.:
% générateur de symboles :
etat9(S) :- retract(cpt(N)) , !, name(N , ASCII), name(S , [115 | ASCII]), N9 is N+1, assert(cpt(N9)).
etat9(s0) :- assert(cpt(1)).
% régles d'inférences en Prolog :
construction A.F. Thompson
conc(E1 , E2) '-ER2AF->' m(S, I , [d(Sf1 , [] , SD2)|D], SD1, [Sf2]) :- !,
E1 '-ER2AF->' m(S1, I1 , D1, SD1, [Sf1]) ,
E2 '-ER2AF->' m(S2, I2 , D2, SD2, [Sf2]) ,
append(S1 , S2 , S) , append(D1 , D2 , D) , append(I1 , I2 , II) , sort(II , I).
ou(E1 , E2) '-ER2AF->' m([SD , Sf|S], I , [d(SD , [] , SD1) , d(SD , [] , SD2) , d(Sf1 , [] , Sf) , d(Sf2 , [] , Sf)|D], SD, [Sf]) :- !,
etat9(SD) , etat9(Sf),
E1 '-ER2AF->' m(S1, I1 , D1, SD1, [Sf1]) ,
E2 '-ER2AF->' m(S2, I2 , D2, SD2, [Sf2]) ,
append(S1 , S2 , S) , append(D1 , D2 , D) , append(I1 , I2 , II) , sort(II , I).
star(E1) '-ER2AF->' m(S1, I1 , [d(SD , [] , SD1) , d(SD , [] , Sf) , d(Sf1 , [] , SD1) , d(Sf1 , [] , Sf)|D1], SD, [Sf]) :- !,
etat9(SD) , etat9(Sf),
E1 '-ER2AF->' m(S1, I1 , D1, SD1, [Sf1]) .
A '-ER2AF->' m([SD,Sf], [A] , [d(SD,A,Sf)], SD, [Sf]) :- not member(A , ['(' , '[' ,
'|' , '*' , ']' , ')']) ,
etat9(SD) , etat9(Sf).
|
QUESTION 8 : ajoutez au programme ci dessus la règle d'inférence pour la définition opt(E) et montrez la réponse de Prolog à la question :
?- lexER('(a|b)*abb' , LCARAC) , er(AST , LCARAC , []) , AST '-ER2AF->' M.
Tout ensemble et génération du "code" Prolog :
il reste, en effet, à générer le code Prolog pour pouvoir reconnaitre si une chaîne est élément de l'ensemble décrit par une ER : reconn(ER , CHAINE).
geneAFProlog(m(_,I,D,S0,SF)) :-
assert(alphabet(I)),
geneTransitions(D),
assert(depart(S0)),
assert(finals(SF)).
geneTransitions([]) :- !.
geneTransitions([T|D]) :- assert(T), geneTransitions(D).
reconn(ER , CHAINE) :- % à cha que question on reconstruit l'AF et on généère le Prolog...
lexER(ER , LCAR) ,
er(AST , LCAR , []) ,
AST '-ER2AF->' M ,
geneAFProlog(M) ,
reconnaissance(CHAINE).
|
QUESTION 9 : quelles réponses à
?- reconn('(a|b)*abb' , [a,b,a,b,a,b,a,b,a,b,a,b,a,b,b,a,b,b,b]) .
?- reconn('(a|b)*abb' , [a,b,a,b,a,b,a,b,a,b,a,b,a,b,b,a,b,b]) .
LCARAC = ['(', a, ('|'), b, ')', *, a, b, b, *] ;
No
er --> tr , ['|'] , er . % L'ER est un Terme
Régulier (tr) ou une ER
er --> tr. % L'ER est un Terme i.e. sans le symbole '|' sauf
entre '(' et ')'
tr --> fr , tr . % Le tr est un Facteur Régulier (fr) concaténé
à un tr
tr --> fr. % Le tr est un simple Facteur Régulier (fr)
fr --> [X] , { not member(X , ['(' , '[' , '|' , '*' ,
']' , ')']) } , fer. % X n'est pas un symbole spécial
fr --> ['('] , er , [')'] , fer. % Le fr est une er entre '(' et
')' suivie d'étoiles
fr --> ['['] ,er,[']'].
fer --> ['*'] , fer. %des *, au moins une
fer --> []. % la chaine vide
LCARAC = ['(', a, ('|'), b, ')', *, a, '[', b, ']', b] ;
No
LCAR = ['(', a, ('|'), b, ')', *, a, b, b, *]
AST = conc(star(ou(a, b)), conc(a, conc(b, star(b)))) ;
No
er --> tr. % L'ER est un Terme i.e. sans le symbole '|' sauf entre '(' et ')'
tr --> fr , tr . % Le tr est un Facteur Régulier (fr) concaténé
à un tr
tr --> fr. % Le tr est un simple Facteur Régulier (fr)
fr --> [X] , { not member(X , ['(' , '[' , '|' , '*' ,
']' , ')']) } , fer. % X n'est pas un symbole spécial
fr --> ['('] , er , [')'] , fer. % Le fr est une er entre '(' et
')' suivie d'étoiles
fr --> ['['] ,er,[']'].
fer --> ['*'] , fer. %des *, au moins une
fer --> []. % la chaine vide
er(ou(TAST , EAST)) --> tr(TAST) , ['|'] , er(EAST) .
er(AST) --> tr(AST).
tr(conc(FAST , TAST)) --> fr(FAST) , tr(TAST) .
tr(AST) --> fr(AST).
fr(AST) --> [X] , { member(X , [a,b]) } , fer(ETOILE) , {zeroOUune(X
, ETOILE , AST)}.
fr(AST) --> ['('] , er(AST1) , [')'] , fer(ETOILE) , {zeroOUune(AST1
, ETOILE , AST)}.
fr(opt(AST)) --> ['['] ,er(AST),[']'].
fer('*') --> ['*'] , fer(_). %une ou plusieurs * est
équivalent à une
fer([]) --> [].
zeroOUune(AST , * , star(AST)).
zeroOUune(AST , [] , AST).
LCAR = ['(', a, ('|'), b, ')', *, a, '[', b, ']', b]
AST = conc(star(ou(a, b)), conc(a, conc(opt(b), b))) ;
No
Yes
I = {0,1}
d ={d(q0,0) = q1,d(q0,1) = q2,d(q1,1)=q3,d(q2,0)=q4,d(q3,0)=q4,d(q3,0)=q5,d(q4,1)=q3,d(q4,1)=q5}
s0 = q0
F = {q5}
finals([q5]).
d(q0,0,q1).
d(q0,1,q2).
d(q1,1,q3).
d(q2,0,q4).
d(q3,0,q4).
d(q3,0,q5).
d(q4,1,q3).
d(q4,1,q5).
- ?- reconnaissance([0,1,0]).
Yes
- ?-
reconnaissance([0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0]).
Yes
opt(E)
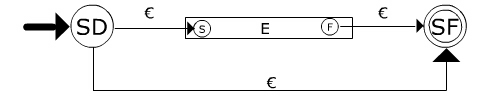
dE v {d(sD,^)=sf , d(sD,^)=s , d(f,^)=s},
sD, {sf})
%construction A.F. Thompson
conc(E1 , E2) '-ER2AF->' m(S, I , [d(Sf1 , [] , SD2)|D],
SD1, [Sf2]) :- !,
E1 '-ER2AF->' m(S1, I1 , D1, SD1, [Sf1]) ,
E2 '-ER2AF->' m(S2, I2 , D2, SD2, [Sf2]) ,
append(S1 , S2 , S) , append(D1 , D2 , D) , append(I1 , I2 , II)
, sort(II , I).
ou(E1 , E2) '-ER2AF->' m([SD , Sf|S], I , [d(SD , [] , SD1) , d(SD
, [] , SD2) , d(Sf1 , [] , Sf) , d(Sf2 , [] , Sf)|D], SD, [Sf])
:- !,
etat9(SD) , etat9(Sf),
E1 '-ER2AF->' m(S1, I1 , D1, SD1, [Sf1]) ,
E2 '-ER2AF->' m(S2, I2 , D2, SD2, [Sf2]) ,
append(S1 , S2 , S) , append(D1 , D2 , D) , append(I1 , I2 , II)
, sort(II , I).
star(E1) '-ER2AF->' m(S1, I1 , [d(SD , [] , SD1) , d(SD , [] ,
Sf) , d(Sf1 , [] , SD1) , d(Sf1 , [] , Sf)|D1], SD, [Sf]) :- !,
etat9(SD) , etat9(Sf),
E1 '-ER2AF->' m(S1, I1 , D1, SD1, [Sf1]) .
opt(E1) '-ER2AF->' m(S1, I1 , [d(SD , [] , SD1) ,
d(SD , [] , Sf) , d(Sf1 , [] , Sf)|D1], SD, [Sf]) :- !,
E1 '-ER2AF->' m(S1, I1 , D1, SD1, [Sf1]) .
A '-ER2AF->' m([SD,Sf], [A] , [d(SD,A,Sf)], SD, [Sf]) :- not
member(A , ['(' , '[' , '|' , '*' , ']' , ')']) ,
etat9(SD) , etat9(Sf).
LCARAC = ['(', a, ('|'), b, ')', *, a, b, b]
AST = conc(star(ou(a, b)), conc(a, conc(b, b)))
M = m([s2, s3, s4, s5, s6, s7, s8, s9, s10, s11, s12, s13], [a,
b], [d(s1, [], s8), d(s0, [], s2), d(s0, [], s1), d(s3, [], s2),
d(s3, [], s1), d(s2, [], s4), d(s2, [], s6), d(s5, [], s3),
d(s7, [], s3), d(s4, a, s5), d(s6, b, s7), d(s9, [], s10), d(s8,
a, s9), d(s11, [], s12), d(s10, b, s11), d(s12, b, s13)], s0,
[s13])
Yes
No
Yes
FIN_dh10
ACCUEIL CONTACT FAVORIS ANNALES DH1 DH2 DH3 DH4 DH5 DH6 DH7 DH8 DH9 DH10 DH11 DH12 DH13 DH14 DH15 DH16