Devoirs Hebdomadaire N°4
CDL...DH4
DJ-Prover & TabSem
Soit montrer le séquent : {p <-> (k & a) v b , k , a <-> (d & c) v e , b <-> ~a , d , ~ c , ~ e} |- ~a
Calcul des Séquents et DJ-Prover : Vous avez téléchargé depuis longtemps DJ-prover.zip.
Son déploiement donne entre autres les 2 fichiers : DJ-prover.pl l'éditeur de preuves et pbprop.djp un fichier texte d'exemples d'énoncés propositionnels.
Un mode d'emploi du DJ-prover se trouve en DJ-prover.html.
Mettre le séquent : {p <-> (k & a) v b , k , a <-> (d & c) v e , b <-> ~a , d , ~ c , ~ e} |- ~a dans la syntaxe exacte pour le DJ-Prover et l'ajouter dans le fichier pbprop.djp comme énoncé n° 66 i.e. ajouter ddans le fichier prouver(66 , ...à completer par le séquent ...).
Lancer le DJ-prover par un double clic sur DJ-prover.pl.
Consulter alors pbprop.djp par la directive ?- ['pbprop.djp'].
Corriger et recharger pbprop.djp jusqu'à ne plus avoir d'erreur de syntaxe.
QUESTION 1 : Vérifer par ?- prouver(66 , P). que le Problème 66 est bien le problème posé et réaliser la démonstration demandée avec DJ-Prover.
Remarque : on lance la démonstration par ?- prouver(66 , P) , P. ATTENTION détruire le fichier trace.dem entre deux essais de preuve
(répondre par la réponse Prolog à ?- prouver(66 , P) et par le contenu du fichier trace.dem généré pendant la preuve).
Tableaux sémantiques et TabSem : ATTENTION : la syntaxe pour TabSem est légèrement différente de celle utilisée pour DJ-Prover
si vous ne disposez pas encore de Java sur votre machine, répondez "à la main" par le tableau sémantique de la preuve. Sinon, Java étant installé, téléchargez TabSem.zip , déployez cette archive. L'application TabSem se lance par un double-clic sur Ee.bat du répertoire généré.
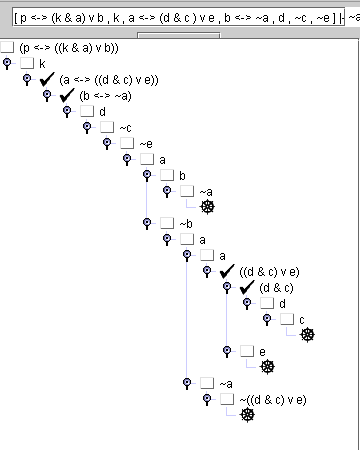
QUESTION 2 : Réaliser avec TabSem la preuve du séquent {p <-> (k & a) v b , k , a <-> (d & c) v e , b <-> ~a , d , ~ c , ~ e} |- ~a . ATTENTION : donner l'énoncé syntaxiquement correct à soumettre à TabSem pour faire cette démonstration.
(répondre par l'image du tableau complètement fermé)
Calcul des Séquents et DJ-Prover :
QUESTION 3 : répondre au problème 44 avec DJ-Prover. Montrer l'énoncé du problème par ?- prouver(44 , P44). puis lancer la démonstration par ?- prouver(44 , P44) , P44.
(répondre par la réponse Prolog à ?- prouver(44 , P44) et par le contenu du fichier trace.dem généré pendant la preuve).
ATTENTION : détruire le fichier trace.dem avant chaque preuve
Tableaux sémantiques et TabSem :
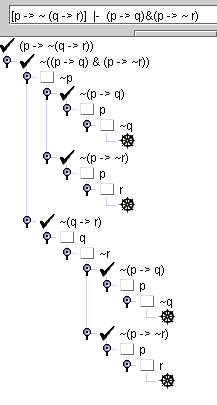
QUESTION 4 : faire la preuve du problème 44 avec TabSem .
(rendre une image)
Q1 : P=[~k v ~a v p , ~b v p , k , ~d v ~c v a , ~e v a , b , d] |- ~a
---------------- démonstration ------------------------------------------------------
Soit prouver :
|
| h(1) :: p<->k&a v b
| h(2) :: k
| h(3) :: a<->d&c v e
| h(4) :: b<-> ~a
| h(5) :: d
| h(6) :: ~c
| h(7) :: ~e
| |-
| c(1) :: ~a
les règles applicables sont: 0 : retour arrière ,
1:intro. lemme, 2: reec. par equivalence, 3: conjecture,
4:(h(1),<->|-),5:(h(3),<->|-),6:(h(4),<->|-),7:(h(6),~|-),8:(h(7),~|-),9:(c(1),|-~).
votre choix ?:6
|
|| par <-> |- : 11 (différée) et : 11
|| h(1) :: p<->k&a v b
|| h(2) :: k
|| h(3) :: a<->d&c v e
|| h(4) :: d
|| h(5) :: ~c
|| h(6) :: ~e
|| |-
|| c(1) :: ~a
|| c(2) :: b
|| c(3) :: ~a
les règles applicables sont: 0 : retour arrière ,
1: intro. lemme, 2: reec. par equivalence, 3: conjecture,
4:(h(1),<->|-),5:(h(3),<->|-),6:(h(5),~|-),7:(h(6),~|-),8:(c(1),|-~),9:(c(3),|-~).
votre choix ?:9
||
||| par |- ~ : 111
||| h(1) :: p<->k&a v b
||| h(2) :: k
||| h(3) :: a<->d&c v e
||| h(4) :: d
||| h(5) :: ~c
||| h(6) :: ~e
||| h(7) :: a
||| |-
||| c(1) :: ~a
||| c(2) :: b
les règles applicables sont: 0 : retour arrière ,
1: intro. lemme, 2: reec. par equivalence, 3: conjecture,
4: (h(1), <->|-), 5: (h(3),<->|-),6:(h(5),~|-),7:(h(6),~|-),8:(c(1),|-~).
votre choix ?:5
|||
|||| par <-> |- : 1111 (différée) et : 1111
|||| h(1) :: p<->k&a v b
|||| h(2) :: k
|||| h(3) :: d
|||| h(4) :: ~c
|||| h(5) :: ~e
|||| h(6) :: a
|||| |-
|||| c(1) :: ~a
|||| c(2) :: b
|||| c(3) :: a
|||| c(4) :: d&c v e
||||| simplification à droite : 11111
||||| h(1), h(2), h(3), h(4), h(5), h(6)
||||| |-
||||| c(1) :: a
|||||| 111111 simplification à gauche et par hypothèse : OK
|||| par <-> |- : 1111 (précédemment différée)
|||| h(1) :: p<->k&a v b
|||| h(2) :: k
|||| h(3) :: d
|||| h(4) :: ~c
|||| h(5) :: ~e
|||| h(6) :: a
|||| h(7) :: a
|||| h(8) :: d&c v e
|||| |-
|||| c(1) :: ~a
|||| c(2) :: b
les règles applicables sont: 0 : retour arrière ,
1: intro. lemme, 2: reec. par equivalence, 3: conjecture,
4: (h(8), v|-), 5:(h(1), <->|-),6:(h(4),~|-),7: (h(5),~|-), 8:(c(1),|-~).
votre choix ?:4
||||
||||| par v|- : 11111 (différée) et : 21111
||||| h(1) :: p<->k&a v b
||||| h(2) :: k
||||| h(3) :: d
||||| h(4) :: ~c
||||| h(5) :: ~e
||||| h(6) :: a
||||| h(7) :: a
||||| h(8) :: e
||||| |-
||||| c(1) :: ~a
||||| c(2) :: b
les règles applicables sont: 0 : retour arrière ,
1: intro. lemme, 2: reec. par equivalence, 3: conjecture,
4: (h(1), <->|-), 5: (h(4), ~|-), 6: (h(5), ~|-), 7: (c(1), |-~).
votre choix ?:4
|||||
|||||| par <-> |- : 121111 (différée) et : 121111
|||||| h(1) :: k
|||||| h(2) :: d
|||||| h(3) :: ~c
|||||| h(4) :: ~e
|||||| h(5) :: a
|||||| h(6) :: a
|||||| h(7) :: e
|||||| |-
|||||| c(1) :: ~a
|||||| c(2) :: b
|||||| c(3) :: p
|||||| c(4) :: k&a v b
les règles applicables sont: 0 : retour arrière ,
1: intro. lemme, 2: reec. par equivalence, 3: conjecture,
4: (h(3), ~|-), 5: (h(4), ~|-), 6: (c(4), |-v), 7: (c(1), |-~).
votre choix ?:6
||||||
||||||| par |-v : 1121111
||||||| h(1), h(2), h(3), h(4), h(5), h(6), h(7)
||||||| |-
||||||| c(1) :: ~a
||||||| c(2) :: b
||||||| c(3) :: p
||||||| c(4) :: k&a
||||||| c(5) :: b
les règles applicables sont: 0 : retour arrière ,
1: intro. lemme, 2: reec. par equivalence, 3: conjecture,
4: (h(3), ~|-), 5: (h(4), ~|-), 6: (c(4), |-&), 7: (c(1), |-~).
votre choix ?:6
|||||||
|||||||| par |-& : 11121111 ( différée) et : 21121111
|||||||| h(1), h(2), h(3), h(4), h(5), h(6), h(7)
|||||||| |-
|||||||| c(1) :: ~a
|||||||| c(2) :: b
|||||||| c(3) :: p
|||||||| c(4) :: b
|||||||| c(5) :: a
||||||||| simplification à droite : 121121111
||||||||| h(1), h(2), h(3), h(4), h(5), h(6), h(7)
||||||||| |-
||||||||| c(1) :: a
|||||||||| 1121121111 simplification à gauche et par hypothèse : OK
|||||||| par |-& : 11121111 (précédemment différée)
|||||||| h(1) :: k
|||||||| h(2) :: d
|||||||| h(3) :: ~c
|||||||| h(4) :: ~e
|||||||| h(5) :: a
|||||||| h(6) :: a
|||||||| h(7) :: e
|||||||| |-
|||||||| c(1) :: ~a
|||||||| c(2) :: b
|||||||| c(3) :: p
|||||||| c(4) :: b
|||||||| c(5) :: k
||||||||| simplification à droite : 111121111
||||||||| h(1), h(2), h(3), h(4), h(5), h(6), h(7)
||||||||| |-
||||||||| c(1) :: k
|||||||||| 1111121111 simplification à gauche et par hypothèse : OK
|||||| par <-> |- : 121111 (précédemment différée)
|||||| h(1) :: k
|||||| h(2) :: d
|||||| h(3) :: ~c
|||||| h(4) :: ~e
|||||| h(5) :: a
|||||| h(6) :: a
|||||| h(7) :: e
|||||| h(8) :: p
|||||| h(9) :: k&a v b
|||||| |-
|||||| c(1) :: ~a
|||||| c(2) :: b
les règles applicables sont: 0 : retour arrière ,
1: intro. lemme, 2: reec. par equivalence, 3: conjecture,
4: (h(9), v|-), 5: (h(3), ~|-), 6: (h(4), ~|-), 7: (c(1), |-~).
votre choix ?:6
||||||
||||||| par ~ |- : 1121111
||||||| h(1) :: k
||||||| h(2) :: d
||||||| h(3) :: ~c
||||||| h(4) :: a
||||||| h(5) :: a
||||||| h(6) :: e
||||||| h(7) :: p
||||||| h(8) :: k&a v b
||||||| |-
||||||| c(1) :: ~a
||||||| c(2) :: b
||||||| c(3) :: e
|||||||| simplification à droite : 11121111
|||||||| h(1), h(2), h(3), h(4), h(5), h(6), h(7), h(8)
|||||||| |-
|||||||| c(1) :: e
||||||||| 111121111 simplification à gauche et par hypothèse : OK
||||| par v|- : 11111 (précédemment différée)
||||| h(1) :: p<->k&a v b
||||| h(2) :: k
||||| h(3) :: d
||||| h(4) :: ~c
||||| h(5) :: ~e
||||| h(6) :: a
||||| h(7) :: a
||||| h(8) :: d&c
||||| |-
||||| c(1) :: ~a
||||| c(2) :: b
les règles applicables sont: 0 : retour arrière ,
1: intro. lemme, 2: reec. par equivalence, 3: conjecture,
4: (h(8), &|-), 5: (h(1), <->|-), 6: (h(4),~|-), 7: (h(5),~|-), 8: (c(1),|-~).
votre choix ?:4
|||||
|||||| par &|- : 111111
|||||| h(1) :: p<->k&a v b
|||||| h(2) :: k
|||||| h(3) :: d
|||||| h(4) :: ~c
|||||| h(5) :: ~e
|||||| h(6) :: a
|||||| h(7) :: a
|||||| h(8) :: d
|||||| h(9) :: c
|||||| |-
|||||| c(1) :: ~a
|||||| c(2) :: b
les règles applicables sont: 0 : retour arrière ,
1: intro. lemme, 2: reec. par equivalence, 3: conjecture,
4: (h(1), <->|-), 5: (h(4), ~|-), 6: (h(5), ~|-), 7: (c(1), |-~).
votre choix ?:4
||||||
||||||| par <-> |- : 1111111 (différée) et : 1111111
||||||| h(1) :: k
||||||| h(2) :: d
||||||| h(3) :: ~c
||||||| h(4) :: ~e
||||||| h(5) :: a
||||||| h(6) :: a
||||||| h(7) :: d
||||||| h(8) :: c
||||||| |-
||||||| c(1) :: ~a
||||||| c(2) :: b
||||||| c(3) :: p
||||||| c(4) :: k&a v b
les règles applicables sont: 0 : retour arrière ,
1: intro. lemme, 2: reec. par equivalence, 3: conjecture,
4: (h(3), ~|-), 5: (h(4), ~|-), 6: (c(4), |-v), 7: (c(1), |-~).
votre choix ?:6
|||||||
|||||||| par |-v : 11111111
|||||||| h(1), h(2), h(3), h(4), h(5), h(6), h(7), h(8)
|||||||| |-
|||||||| c(1) :: ~a
|||||||| c(2) :: b
|||||||| c(3) :: p
|||||||| c(4) :: k&a
|||||||| c(5) :: b
les règles applicables sont: 0 : retour arrière ,
1: intro. lemme, 2: reec. par equivalence, 3: conjecture,
4: (h(3), ~|-), 5: (h(4), ~|-), 6: (c(4), |-&), 7: (c(1), |-~).
votre choix ?:6
||||||||
||||||||| par |-& : 111111111 ( différée) et : 211111111
||||||||| h(1), h(2), h(3), h(4), h(5), h(6), h(7), h(8)
||||||||| |-
||||||||| c(1) :: ~a
||||||||| c(2) :: b
||||||||| c(3) :: p
||||||||| c(4) :: b
||||||||| c(5) :: a
|||||||||| simplification à droite : 1211111111
|||||||||| h(1), h(2), h(3), h(4), h(5), h(6), h(7), h(8)
|||||||||| |-
|||||||||| c(1) :: a
||||||||||| 11211111111 simplification à gauche et par hypothèse : OK
||||||||| par |-& : 111111111 (précédemment différée)
||||||||| h(1) :: k
||||||||| h(2) :: d
||||||||| h(3) :: ~c
||||||||| h(4) :: ~e
||||||||| h(5) :: a
||||||||| h(6) :: a
||||||||| h(7) :: d
||||||||| h(8) :: c
||||||||| |-
||||||||| c(1) :: ~a
||||||||| c(2) :: b
||||||||| c(3) :: p
||||||||| c(4) :: b
||||||||| c(5) :: k
|||||||||| simplification à droite : 1111111111
|||||||||| h(1), h(2), h(3), h(4), h(5), h(6), h(7), h(8)
|||||||||| |-
|||||||||| c(1) :: k
||||||||||| 11111111111 simplification à gauche et par hypothèse : OK
||||||| par <-> |- : 1111111 (précédemment différée)
||||||| h(1) :: k
||||||| h(2) :: d
||||||| h(3) :: ~c
||||||| h(4) :: ~e
||||||| h(5) :: a
||||||| h(6) :: a
||||||| h(7) :: d
||||||| h(8) :: c
||||||| h(9) :: p
||||||| h(10) :: k&a v b
||||||| |-
||||||| c(1) :: ~a
||||||| c(2) :: b
les règles applicables sont: 0 : retour arrière ,
1: intro. lemme, 2: reec. par equivalence, 3: conjecture,
4: (h(10), v|-), 5: (h(3), ~|-), 6: (h(4), ~|-), 7: (c(1), |-~).
votre choix ?:4
|||||||
|||||||| par v|- : 11111111 (différée) et : 21111111
|||||||| h(1) :: k
|||||||| h(2) :: d
|||||||| h(3) :: ~c
|||||||| h(4) :: ~e
|||||||| h(5) :: a
|||||||| h(6) :: a
|||||||| h(7) :: d
|||||||| h(8) :: c
|||||||| h(9) :: p
|||||||| h(10) :: b
|||||||| |-
|||||||| c(1) :: ~a
|||||||| c(2) :: b
||||||||| simplification à droite : 121111111
||||||||| h(1), h(2), h(3), h(4), h(5), h(6), h(7), h(8), h(9), h(10)
||||||||| |-
||||||||| c(1) :: b
|||||||||| 1121111111 simplification à gauche et par hypothèse : OK
|||||||| par v|- : 11111111 (précédemment différée)
|||||||| h(1) :: k
|||||||| h(2) :: d
|||||||| h(3) :: ~c
|||||||| h(4) :: ~e
|||||||| h(5) :: a
|||||||| h(6) :: a
|||||||| h(7) :: d
|||||||| h(8) :: c
|||||||| h(9) :: p
|||||||| h(10) :: k&a
|||||||| |-
|||||||| c(1) :: ~a
|||||||| c(2) :: b
les règles applicables sont: 0 : retour arrière ,
1: intro. lemme, 2: reec. par equivalence, 3: conjecture,
4: (h(10), &|-), 5: (h(3), ~|-), 6: (h(4), ~|-), 7: (c(1), |-~).
votre choix ?:4
||||||||
||||||||| par &|- : 111111111
||||||||| h(1) :: k
||||||||| h(2) :: d
||||||||| h(3) :: ~c
||||||||| h(4) :: ~e
||||||||| h(5) :: a
||||||||| h(6) :: a
||||||||| h(7) :: d
||||||||| h(8) :: c
||||||||| h(9) :: p
||||||||| h(10) :: k
||||||||| h(11) :: a
||||||||| |-
||||||||| c(1) :: ~a
||||||||| c(2) :: b
les règles applicables sont: 0 : retour arrière ,
1: intro. lemme, 2: reec. par equivalence, 3: conjecture,
4: (h(3), ~|-), 5: (h(4), ~|-), 6: (c(1), |-~).
votre choix ?:4
|||||||||
|||||||||| par ~ |- : 1111111111
|||||||||| h(1) :: k
|||||||||| h(2) :: d
|||||||||| h(3) :: ~e
|||||||||| h(4) :: a
|||||||||| h(5) :: a
|||||||||| h(6) :: d
|||||||||| h(7) :: c
|||||||||| h(8) :: p
|||||||||| h(9) :: k
|||||||||| h(10) :: a
|||||||||| |-
|||||||||| c(1) :: ~a
|||||||||| c(2) :: b
|||||||||| c(3) :: c
||||||||||| simplification à droite : 11111111111
||||||||||| h(1), h(2), h(3), h(4), h(5), h(6), h(7), h(8), h(9), h(10)
||||||||||| |-
||||||||||| c(1) :: c
|||||||||||| 111111111111 simplification à gauche et par hypothèse : OK
|| par <-> |- : 11 (précédemment différée)
|| h(1) :: p<->k&a v b
|| h(2) :: k
|| h(3) :: a<->d&c v e
|| h(4) :: d
|| h(5) :: ~c
|| h(6) :: ~e
|| h(7) :: b
|| h(8) :: ~a
|| |-
|| c(1) :: ~a
||| 111 simplification à gauche et par hypothèse : OK
cqfd
Q2 :
Q3 :
Soit prouver :
|
| h(1) :: p-> ~ (q->r)
| |-
| c(1) :: (p->q)& (p-> ~r)
les règles applicables sont: 0 : retour arrière ,
1: intro. lemme, 2: reec. par equivalence, 3: conjecture,
4: (h(1), ->|-), 5: (c(1), |-&).
votre choix ?:4
|
|| par -> |- : 11 (différée) et : 21
|| h(1) :: ~ (q->r)
|| |-
|| c(1) :: (p->q)& (p-> ~r)
les règles applicables sont: 0 : retour arrière ,
1: intro. lemme, 2: reec. par equivalence, 3: conjecture,
4: (h(1), ~|-), 5: (c(1), |-&).
votre choix ?:4
||
||| par ~ |- : 121
|||
||| |-
||| c(1) :: (p->q)& (p-> ~r)
||| c(2) :: q->r
les règles applicables sont: 0 : retour arrière ,
1: intro. lemme, 2: reec. par equivalence, 3: conjecture,
4: (c(1), |-&), 5: (c(2), |-->).
votre choix ?:5
|||
|||| par |- -> : 1121
|||| h(1) :: q
|||| |-
|||| c(1) :: (p->q)& (p-> ~r)
|||| c(2) :: r
||||| par |-& : 11121 ( différée) et : 21121
||||| h(1)
||||| |-
||||| c(1) :: r
||||| c(2) :: p-> ~r
|||||| par |- -> : 121121
|||||| h(1) :: q
|||||| h(2) :: p
|||||| |-
|||||| c(1) :: r
|||||| c(2) :: ~r
||||||| par |- ~ : 1121121
||||||| h(1) :: q
||||||| h(2) :: p
||||||| h(3) :: r
||||||| |-
||||||| c(1) :: r
|||||||| 11121121 simplification à gauche et par hypothèse : OK
||||| par |-& : 11121 (précédemment différée)
||||| h(1) :: q
||||| |-
||||| c(1) :: r
||||| c(2) :: p->q
|||||| par |- -> : 111121
|||||| h(1) :: q
|||||| h(2) :: p
|||||| |-
|||||| c(1) :: r
|||||| c(2) :: q
||||||| simplification à droite : 1111121
||||||| h(1), h(2)
||||||| |-
||||||| c(1) :: q
|||||||| 11111121 simplification à gauche et par hypothèse : OK
|| par -> |- : 11 ( précédemment différée)
||
|| |-
|| c(1) :: (p->q)& (p-> ~r)
|| c(2) :: p
||| par |-& : 111 ( différée) et : 211
|||
||| |-
||| c(1) :: p
||| c(2) :: p-> ~r
|||| par |- -> : 1211
|||| h(1) :: p
|||| |-
|||| c(1) :: p
|||| c(2) :: ~r
||||| simplification à droite : 11211
||||| h(1)
||||| |-
||||| c(1) :: p
|||||| 111211 par hypothèse : ok
||||||
||| par |-& : 111 (précédemment différée)
|||
||| |-
||| c(1) :: p
||| c(2) :: p->q
|||| par |- -> : 1111
|||| h(1) :: p
|||| |-
|||| c(1) :: p
|||| c(2) :: q
||||| simplification à droite : 11111
||||| h(1)
||||| |-
||||| c(1) :: p
|||||| 111111 par hypothèse : ok
||||||
cqfd
|
Q4 :
FIN_dh4
ACCUEIL CONTACT FAVORIS ANNALES DH1 DH2 DH3 DH4 DH5 DH6 DH7 DH8 DH9 DH10 DH11 DH12 DH13 DH14 DH15 DH16