Devoirs Hebdomadaire N°5
CDL...DH5
Soit le programme DATALOG :
| f(a).
h(a,b). g(Z) :- f(Y). |
QUESTION 1 : quel est l'univers de Herbrand de progr1 ?
QUESTION 2 : Calculer la sémantique de point fixe de progr1 (fonction Tp)
QUESTION 3 : Calculer la sémantique en chaînage arrière de ce prog1 en utilisant Prolog.
EXERCICE 2 : DATALOG, Programmation
| Alice est dans la forêt de l'oubli, elle
n'oublie pas tout mais certaines choses l'ennuient beaucoup comme
oublier le jour de la semaine.Dans cette forêt il y a un lion et une
licorne "binaires" i.e. le lion ment les lundis, les mardis et les
mercredis et dit la vérité les autres jours de la semaine et la
licorne ment les jeudis, les vendredis et les samedi et dit la
vérité les autres jours de la semaine. Un jour alice les rencontre
allongés sous un arbre. Elle est très ennuyée, elle a à nouveau
oublié le jour de la semaine, alors elle demande au lion et à la
licorne :
quel jour sommes nous ? Le Lion et la licorne répondent ensemble: Hier je mentais !!! Alice réfléchit un peu et s'en va satisfaite... |
En ED nous avons résolu cette enigme par le programme DATALOG :
%Hier d'aujourd'hui.. hier(mercredi, mardi). hier(mardi, lundi). hier(lundi, dimanche). hier(dimanche, samedi). hier(samedi, vendredi). hier(vendredi, jeudi). hier(jeudi, mercredi). %quand ils mentent... mensonge(licorne, vendredi ). mensonge(licorne, samedi ). mensonge(lion, lundi). mensonge(lion, mardi ). mensonge(lion, mercredi ). mensonge(licorne, jeudi ). %quand ils disent la vérité... vérité(lion, vendredi ). vérité(lion, samedi ). vérité(lion, dimanche ). vérité(licorne, dimanche ). vérité(licorne, lundi). vérité(licorne, mardi ). vérité(licorne, mercredi ). vérité(lion, jeudi ). %quand le lion (ou la licorne) parle d'un jour et dit qu'il mentait ce Jour
quandJeDisQueJeMens(L, Quand, Jour) :-
vérité(L, Quand), mensonge(L,Jour).
quandJeDisQueJeMens(L, Quand, Jour) :-
mensonge(L, Quand ) , vérité(L, Jour ).
|
| % la question d'alice sous trois formes : |
%Questions : question_1_Alice(AUJOURDHUI) :- hier( AUJOURDHUI, HIER), quandJeDisQueJeMens(lion, AUJOURDHUI, HIER), quandJeDisQueJeMens(licorne, AUJOURDHUI, HIER). question_2_Alice(AUJOURDHUI) :- quandJeDisQueJeMens(lion, AUJOURDHUI, HIER), hier( AUJOURDHUI, HIER), quandJeDisQueJeMens(licorne, AUJOURDHUI, HIER). question_3_Alice(AUJOURDHUI) :- quandJeDisQueJeMens(lion, AUJOURDHUI, HIER), quandJeDisQueJeMens(licorne, AUJOURDHUI, HIER) , hier( AUJOURDHUI, HIER). |
QUESTION 1 : Constater que les 3 questions d'Alice donnent le même résultat unique : "jeudi" (répondre par une copie de la session Prolog.)
Donc la place de "hier( AUJOURDHUI, HIER)" dans la queue de règle n'a pas d'importance.
On "améliore" le programme en se débarrassant du prédicat vérité/2 et en utilisant le 'not' Prolog ce qui correspond mieux à l'énoncé ( .... et dit la vérité les autres jours ... )
%Hier d'aujourd'hui.. hier(mercredi, mardi). hier(mardi, lundi). hier(lundi, dimanche). hier(dimanche, samedi). hier(samedi, vendredi). hier(vendredi, jeudi). hier(jeudi, mercredi). %quand ils mentent... mensonge(licorne, vendredi ). mensonge(licorne, samedi ). mensonge(lion, lundi). mensonge(lion, mardi ). mensonge(lion, mercredi ). mensonge(licorne, jeudi ). %quand le lion (ou la licorne) parle d'un jour et dit qu'il mentait ce Jour
quandJeDisQueJeMensNeg(L, Quand, Jour) :-
not mensonge(L, Quand), mensonge(L,Jour).
quandJeDisQueJeMensNeg(L, Quand, Jour) :-
mensonge(L, Quand ) , not mensonge(L, Jour ).
|
| % la question d'alice sous trois formes : |
%Questions : question_neg1_Alice(AUJOURDHUI) :- hier( AUJOURDHUI, HIER), quandJeDisQueJeMensNeg(lion, AUJOURDHUI, HIER), quandJeDisQueJeMensNeg(licorne, AUJOURDHUI, HIER). question_neg2_Alice(AUJOURDHUI) :- quandJeDisQueJeMensNeg(lion, AUJOURDHUI, HIER), hier( AUJOURDHUI, HIER), quandJeDisQueJeMensNeg(licorne, AUJOURDHUI, HIER). question_neg3_Alice(AUJOURDHUI) :- quandJeDisQueJeMensNeg(lion, AUJOURDHUI, HIER), quandJeDisQueJeMensNeg(licorne, AUJOURDHUI, HIER) , hier( AUJOURDHUI, HIER). |
QUESTION 2 : Constater que les 3 questions d'Alice ne donnent pas le même résultat unique : "jeudi" (répondre par une copie de la session Prolog.). Pour quelle raison ? Quelle question est la bonne ?
| Le lion et la licorne s'absentent pendant
un mois pour aller combattre les derniers dinosaures. Mais à cette
époque pincemi et pincemoi sont dans la forêt. Pincemi est comme le
lion et pincemoi comme la licorne, mais Alice ne sait pas qui est
comme qui ni qui est qui car ils sont jumeaux et se ressemblent
complètement. Un jour Alice les rencontre alors qu'elle a à nouveau
oublié le jour de la semaine. A sa question quel jour sommes nous ?
le premier affirme "je suis pincemi" et le second affirme naturellement "je suis pincemoi". Alice réfléchit un peu et s'en va satisfaite... |
QUESTION 3 :
Répondre en Prolog à la question d'Alice en apprenant par la même occasion "Qui est qui ?"
Remarques : On dispose toujours des programmes précédents, mais maintenant on sait :
mensonge(pincemi, J):- mensonge(lion, J).
mensonge(pincemoi, J):- mensonge(licorne, J).
quandJeDisQueJeMensNeg(L, Quand, Jour) n'est pas utile ici. En effet les affirmations des deux font que soit ils mentent tous les deux, soit ils disent vrais tous les deux .
et il faut définir une nouvelle question d'Alice :
questionAlicePP(PREMIER , SECOND , AUJOURDHUI) :- ...
ATTENTION à l'utilisation de la négation, pensez à l'utilisation d'un prédicat comme : jour/1 ci dessous
jour(lundi). jour(mardi). jour(mercredi). jour(jeudi). jour(vendredi). jour(samedi). jour(dimanche). |
EXERCICE 3 : DATALOG, et Base de données
Les réponses aux questions de cet exercice seront données dans un tableau à deux colonnes : colonne de gauche les tuples des relations, les requêtes SQL et le résultat escompté, colonne de droite les faits Prolog et les règles DATALOG et la copie d'une session Prolog avec la question posée et des résultats équivalents aux résultats en colonne de gauche.
Soient les schémas de relations :
AIME(BUVEUR, BIERE)
VEND(BAR, BIERE, PRIX)
FREQUENTE(BUVEUR, BAR)
QUESTION 1 :
imaginez (colonne de gauche) : une Base de Données contenant les 3 tables AIME , VEND , FREQUENTE, chaque table contenant au moins 6 tuples i.e. il y a plusieurs buveurs, plusieurs bars , plusieurs bières à plusieurs prix et dans la colonne de droite l'ensemble de faits DATALOG équivalents.
remarque : un buveur peut aimer plusieurs bières, un bar peut vendre plusieurs bières, une bière peut être vendues à plusieurs prix.
"les buveurs heureux sont des buveurs qui fréquentent des bars qui vendent de la bière qu'ils aiment".
QUESTION 2 : Quels sont les buveurs heureux ? répondez à cette question : colonne de gauche par une requête SQL et colonne de droite en DATALOG par la définition de la règle
buveurHEUREUX(BUVEUR) :- % à compléter...
et la copie de la session Prolog avec toutes les réponses à la question :
?- buveurHEUREUX(BUVEUR).
QUESTION 3 : Quels sont les bars qui vendent 2 bières différentes au même prix ? répondez à cette question : colonne de gauche par une requête SQL et colonne de droite en DATALOG par la définition de la règle
bar2(BAR) :- % à compléter...
et la copie de la session Prolog avec toutes les réponses à la question :
?- bar2(BAR).
Ajouter à la Base de Données la table BIERE(NOM , BRASSEURS) avec au moins 6 tuples.
QUESTION 4 : Quels sont les brasseurs qui fournissent le bar "joe" ? répondez à cette question : colonne de gauche par une requête SQL et colonne de droite en DATALOG par la définition de la règle
barJOE(BRASSEUR) :- % à compléter...
et la copie de la session Prolog avec toutes les réponses à la question :
?- barJOE(B).
EXERCICE 4 : DATALOG, négation
Soit le programme de reconnaisssance de la parité des nombres {0,1,2,3,4}
suc(0,1). suc(1,2). suc(2,3). suc(3,4). pair(0). pair(X) :- suc(Z , Y) , suc(Y,X) , pair(Z). impair(X) :- not pair(X). |
QUESTION 1 :
Donnez l'univers de Herbrand de nbre01234.pl, la cardinalité de sa Base de Herbrand et calculez sa sémantique de point fixe (ATTENTION : du fait de la présence de 'not' il faut stratifier le programme).
Remarque : à la question ?- impair(N) la négation est toujours appliquée de manière NON sûre donc en chaînage arrière on n'atteint pas en Prolog la sémantique 'attendue'.
?- impair(N).
No
?-
Pour retrouver la sémantique attendue i.e. la sémantique identique à celle de point fixe on se donne le prédicat nbre/1 qui va permettre d'instancier la variable sous le not :
nbre(0). nbre(1). nbre(2). nbre(3). nbre(4). |
QUESTION 2 : modifiez le prédicat impair/1 en utilisant nbre/1 et calculez la sémantique en chaînage arrière du programme. (répondre par une copie de la session Prolog).
QUESTION 3 : calculez le complété du programme (y compris les différents axiomes et règles à ajouter aux formules logiques correspondant au programme. ATTENTION : le programme complete.pl ne donne pas ces "suppléments").
EXERCICE -1-
EXERCICE -2-
EXERCICE -3-
EXERCICE -4-
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
FIN_dh5
ACCUEIL CONTACT FAVORIS ANNALES DH1 DH2 DH3 DH4 DH5 DH6 DH7 DH8 DH9 DH10 DH11 DH12 DH13 DH14 DH15 DH16
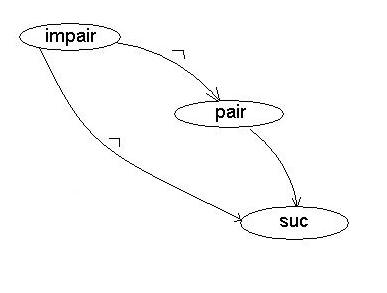 S1 = {pair, suc}
TpS10 = {suc(0 , 1, suc(1 , 2), suc(2 , 3), suc(3 , 4), pair(0)}
TpS11 = TpS10 U {pair(2), pair(4)} = TpS1¥
S1 = {pair, suc}
TpS10 = {suc(0 , 1, suc(1 , 2), suc(2 , 3), suc(3 , 4), pair(0)}
TpS11 = TpS10 U {pair(2), pair(4)} = TpS1¥
 S2 = {impair}
TpS20 = TpS1¥ U {impair(1), impair(3)} = TpS2¥
S2 = {impair}
TpS20 = TpS1¥ U {impair(1), impair(3)} = TpS2¥